VM算法圆查找工具与基于opencv开发的圆查找对比
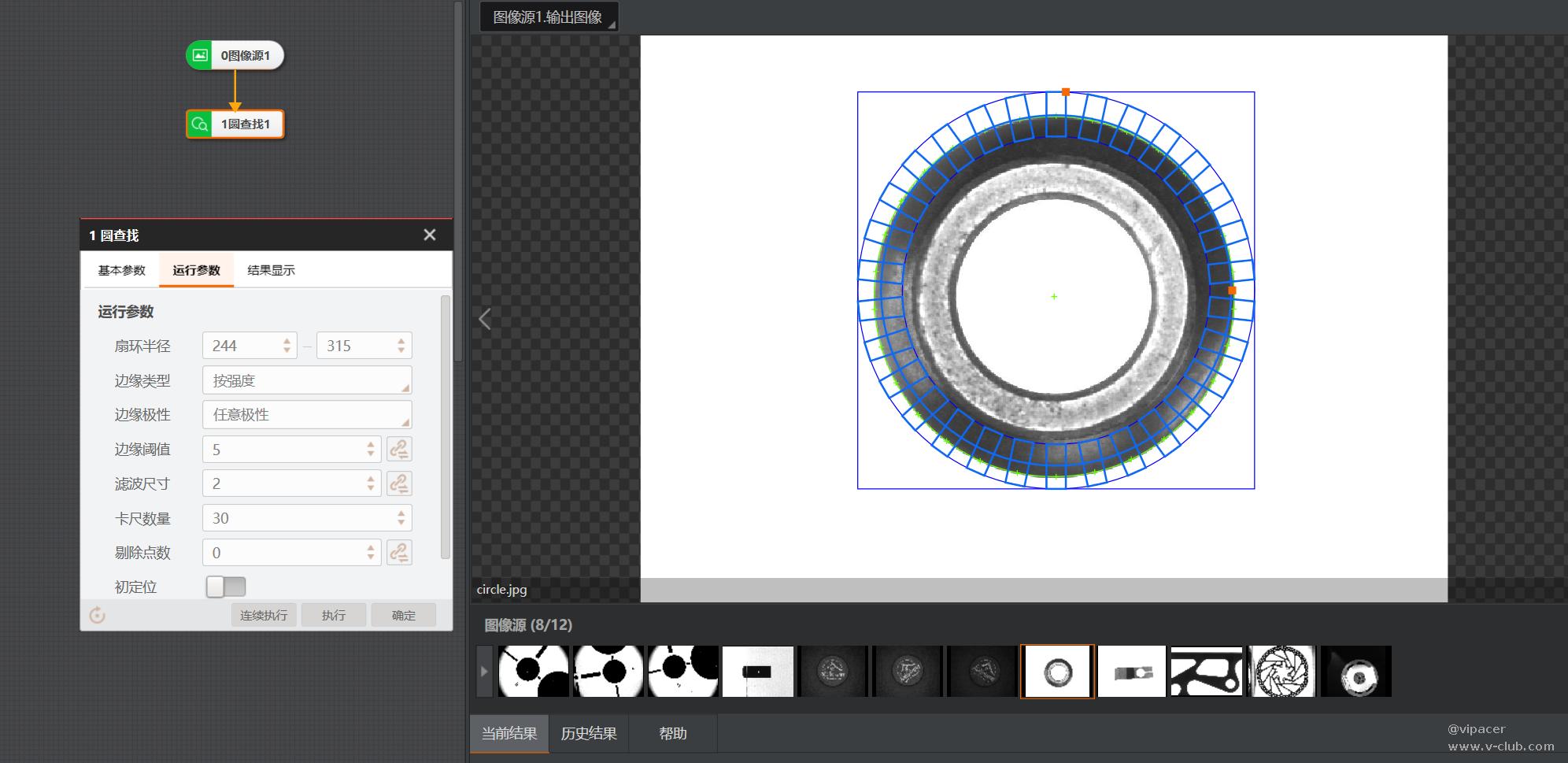
采用opencv开发的卡尺测量圆工具与VM4.3性能对比,博主采用Qt5与opencv开发的卡尺圆测量工具与海康视觉软件VisionMaster4.0的圆查找工具进行性能对比。
卡尺的原理就是找N个小矩形ROI里面的灰度值突变的地方。即:遍历每个小矩形ROI,分别找到1个点,这个点是灰度突变的峰值。然后把这N个点拟合成直线或者圆。
圆拟合是一种用于从给定的离散点集合中拟合出一个最佳的圆形的方法。它在许多领域中都有广泛的应用,例如计算机视觉、几何建模等。
圆拟合的原理通常基于最小二乘法,旨在找到一个圆形模型,使得给定的点集与该圆形模型之间的残差平方和最小。其步骤如下:
数据预处理:首先,对于输入的离散点集合,可以进行一些必要的预处理操作,例如去除异常值或噪声点,确保数据质量。
初始圆形模型估计:为了得到初始的圆形模型,通常可以通过其中的几个点计算出初始的圆心位置和半径估计值。这可以使用一些简单的方法,如三点定圆法(经过任意三个非共线点确定一个圆)或最小二乘法拟合一个初始圆。
最小二乘拟合:在得到初始的圆形模型估计后,使用最小二乘法来优化拟合结果。最小二乘法通过迭代的方式调整圆心位置和半径的值,使得拟合误差最小化。
残差计算和优化:在每次迭代中,根据当前的圆心位置和半径,计算每个点到圆的距离,然后将这些距离的平方和作为拟合误差的度量。根据拟合误差,通过优化算法(如非线性最小二乘法或梯度下降法)更新圆心和半径的值。
收敛判断:对于每次迭代,可以设定一个收敛条件,当满足条件时停止迭代,得到最终的圆形模型。
需要注意的是,圆拟合方法的性能和效果取决于离散点集的分布和噪声程度。对于噪声较多或存在异常点的情况,可能需要使用一些鲁棒性更好的拟合方法,例如 RANSAC(随机抽样一致性)算法来估计圆形模型。
对比1
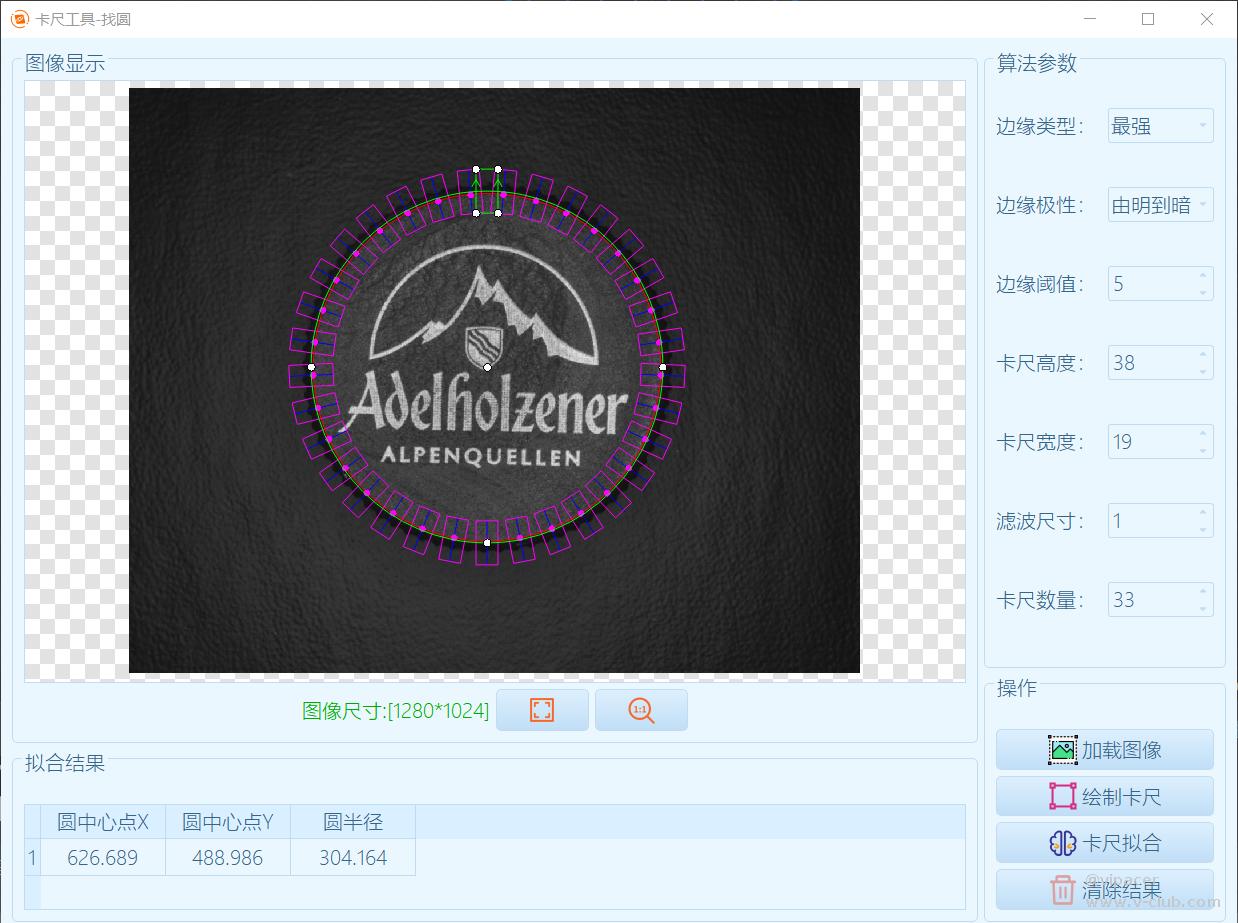

对比2
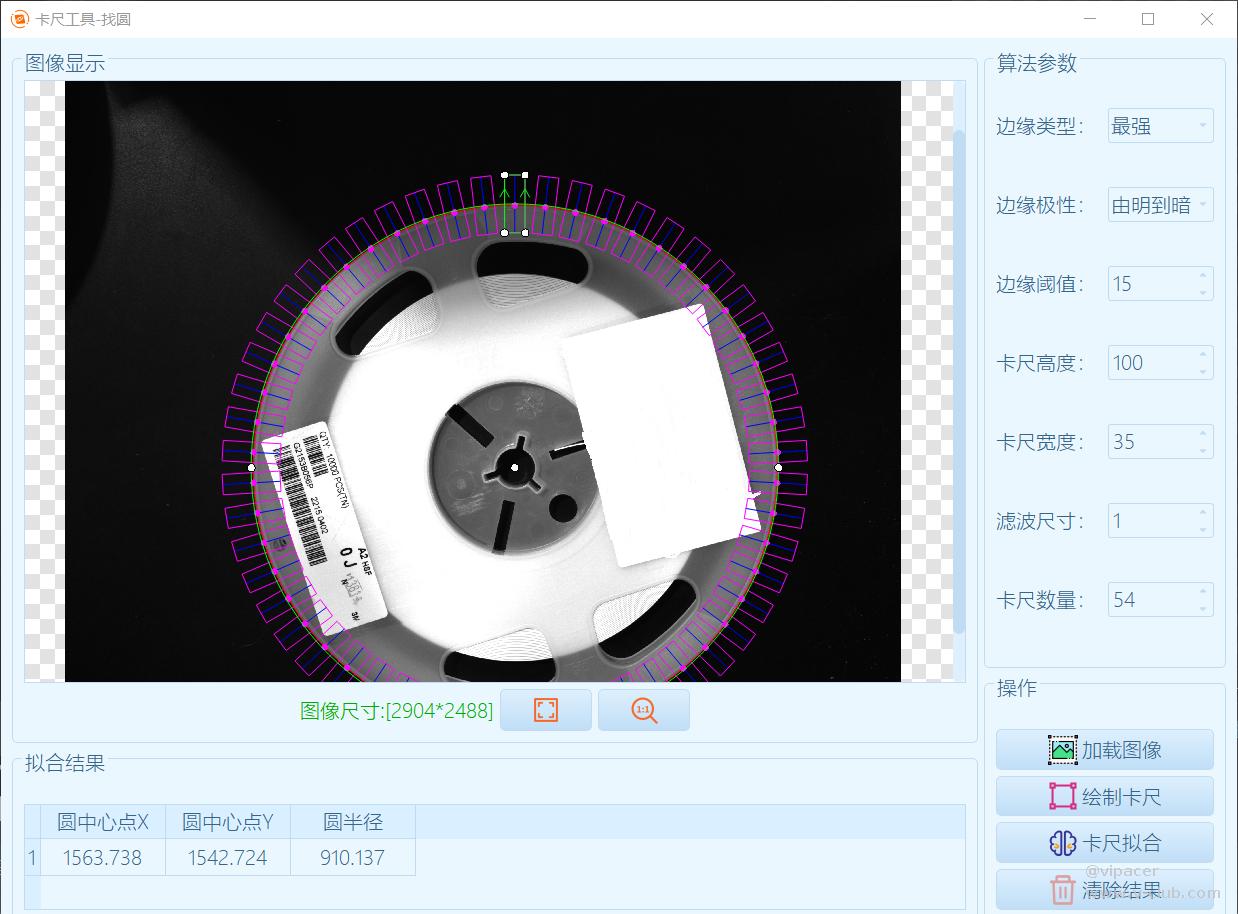
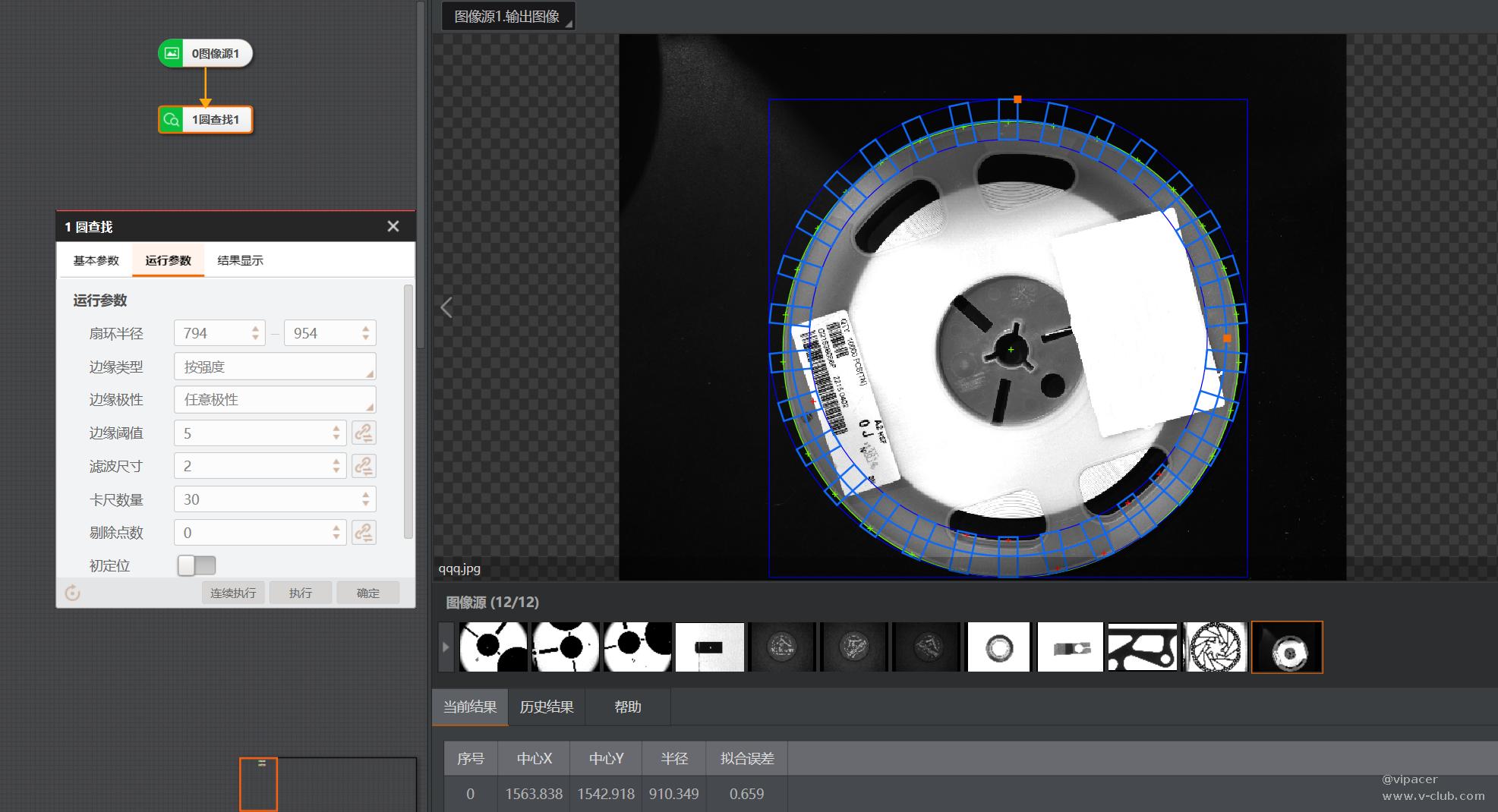
对比3
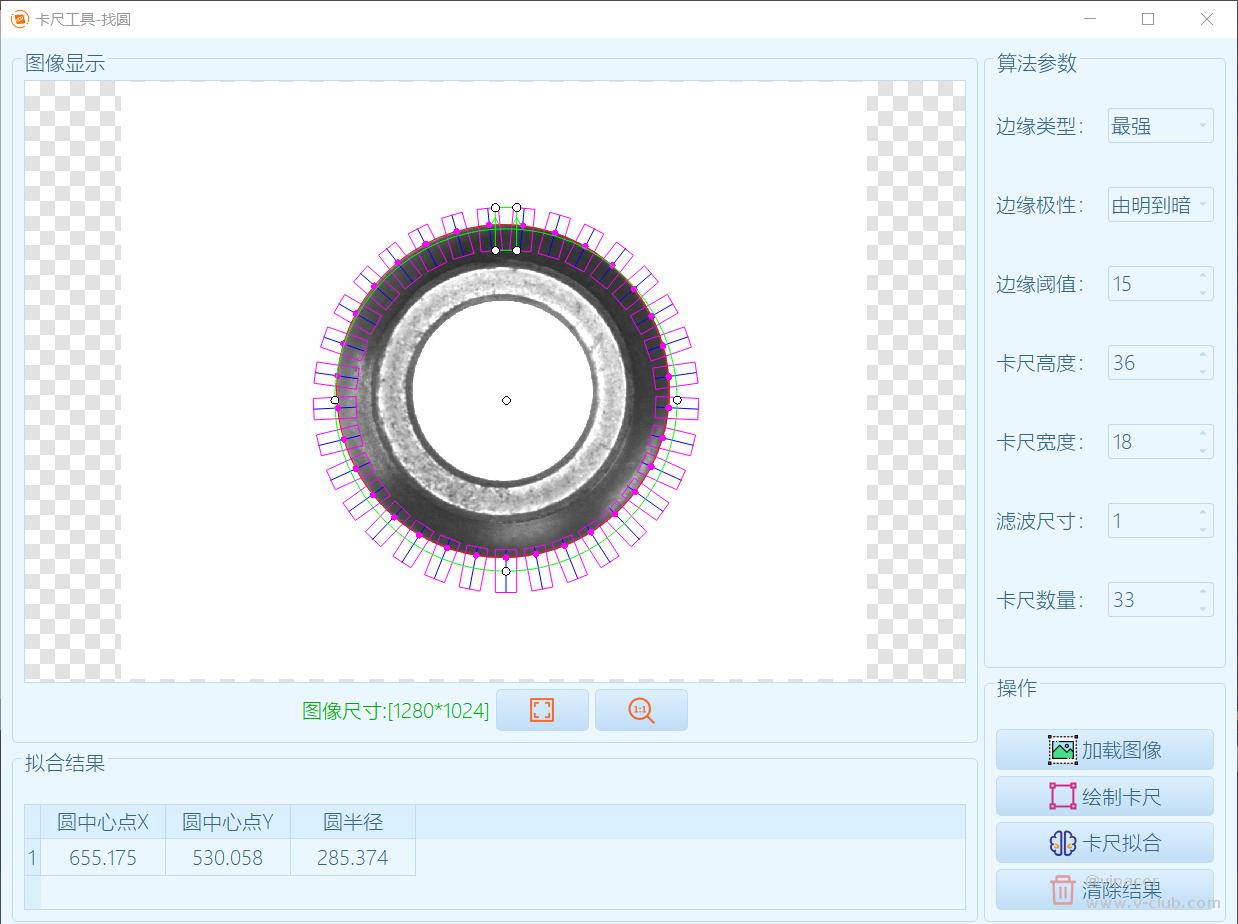
版权声明:本文为V社区用户原创内容,转载时必须标注文章的来源(V社区),文章链接、文章作者等基本信息,否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件至:v-club@hikrobotics.com 进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容。
评论请先登录 登录
全部评论 5
卡尺的原理就是找N个小矩形ROI里面的灰度值突变的地方。即:遍历每个小矩形ROI,分别找到1个点,这个点是灰度突变的峰值。然后把这N个点拟合成直线或者圆
2024-05-31 14:43:10 广东省
回复
1
- 1
相关阅读
 细化梯度2025-11-26
细化梯度2025-11-26 叉车效率优化2025-11-28
叉车效率优化2025-11-28 第四届“启智杯”机器智能大赛红头文件2025-11-28
第四届“启智杯”机器智能大赛红头文件2025-11-28 RCS-2000V4.3.X产品介绍2025-12-11
RCS-2000V4.3.X产品介绍2025-12-11 RCS-2000V4.X国标接口调用DEMO(JAVA)2025-12-15
RCS-2000V4.X国标接口调用DEMO(JAVA)2025-12-15


 浙公网安备 33010802013223号
浙公网安备 33010802013223号