一.扇形的绘制

在Window中，HDC是用于绘图的句柄，它和HWND一样。HDC是设备环境专用的绘图句柄。在MFC中封装于CDC类中。
HDC句柄绘图有三种方式，分别为标准客户区绘图、临时客户区绘图和非客户区绘图。因此CDC类绘图也分为三种，与之对应即标准客户区绘图（CPaintDC）、临时客户区绘图（CClientDC）和非客户区绘图（CWindowDC）。
在CDC类中，没有直接提供用于绘制控件要求的扇形，但提供了绘制椭圆弧和直线的接口，即：

//绘制椭圆弧线 
BOOL Arc(int x1, int y1, int x2, int y2, 
	int x3, int y3, int x4, int y4); 
BOOL Arc(LPCRECT lpRect, POINT ptStart, POINT ptEnd); 
//绘制直线
BOOL Polyline( LPPOINT lpPoints, int nCount);

具体使用如下

m_displayDC->Arc(temp->data->maxRectBoundary, temp->data->anglePoint[0], temp->data->anglePoint[2]);
m_displayDC->Arc(temp->data->minRectBoundary, temp->data->anglePoint[1], temp->data->anglePoint[3]); 
//anglePoint是一个CPoint数组，anglePoint[0]、anglePoint[2]是外圆起止点，anglePoint[1]、anglePoint[3]是内圆起止点
m_displayDC->Polyline(temp->data->anglePoint, 2);
m_displayDC->Polyline((temp->data->anglePoint + 2), 2);

效果如下	

二.点在扇形内的判断

废话不多说，直接上代码

struct S_PIE
{
	CPoint center;
	CRect maxRectBoundary;			//外圆矩形边界，相当于外圆半径
	CRect minRectBoundary;			//内圆矩形边界，相当于内圆半径
	CPoint anglePoint[4];			//顺序为大圆起始，小圆起始，大圆结束，小圆结束
	CPoint maxMiddlePoint;			//大圆弧中点坐标
	CPoint minMiddlePoint;			//小圆弧中点坐标
}; 

struct S_PIEINFO
{
	bool isHover;			//鼠标是否悬浮其上
	int listBoxNum;			//该图形在list内的值
	S_PIEINFO* fNode;		//链表内的前一节点
	S_PIE* data;					
	S_PIEINFO* rNode;		//链表内的后一节点
};

float getAngleToXPositive(CPoint vector) {
	if (vector.x >= 0 && vector.y == 0)
		return 0.0f;
	else if (vector.x == 0 && vector.y > 0)
		return PI / 2;
	else if (vector.x == 0 && vector.y < 0)
		return PI * 3 / 2;
	else if (vector.x < 0 && vector.y == 0)
		return PI;

	float xita = acos(vector.x / sqrt(pow(vector.x, 2) + pow(vector.y, 2)));

	if (vector.y > 0)
		return xita;
	else
		return 2 * PI - xita;
}

bool isInPie(S_PIEINFO* pie, CPoint* currentPoint) {
	int maxR = pie->data->maxRectBoundary.right - pie->data->center.x;
	int minR = pie->data->minRectBoundary.right - pie->data->center.x;
	float r = sqrt(pow(currentPoint->x - pie->data->center.x, 2) + pow(currentPoint->y - pie->data->center.y, 2));

	if (r > maxR || r < minR)
		return 0;
	else {
		//求start点的向量与x轴正向夹角
		CPoint startVector(pie->data->anglePoint[0].x- pie->data->center.x, pie->data->anglePoint[0].y - pie->data->center.y);
		float startAngle = getAngleToXPositive(startVector);

		//求end点的向量与x轴正向夹角
		CPoint endVector(pie->data->anglePoint[2].x - pie->data->center.x, pie->data->anglePoint[2].y - pie->data->center.y);
		float endAngle = getAngleToXPositive(endVector);

		CPoint cPointVector(currentPoint->x - pie->data->center.x, currentPoint->y - pie->data->center.y);
		float cPointAngle = getAngleToXPositive(cPointVector);

		if (cPointAngle >= startAngle && cPointAngle <= endAngle || cPointAngle >= endAngle && cPointAngle <= startAngle)
			return 1;
	}
}

效果如下	

三.扇形的夹角调整事件

矩形与多边形的调整大多是线性的，即矩形或多边形某点的改变只需要：*某点（x或y）+= 当前鼠标位置（x或y）- 前一鼠标位置（x或y）*即可实现。
但扇形夹角的调整却无法这么做，扇形的边界点调整需要将鼠标移动的dx，dy转变为边界点绕圆心的角度。
本文提出一种可行的方法，并以C++代码实现这种线性变换。

1.原理

点绕圆心的旋转可理解为点与圆心所成二维向量绕圆心进行旋转。如下图所示，有一向量OA，其模长为r，将其绕O点旋转θ°得到向量OB，则点B的坐标可由点A表示为 

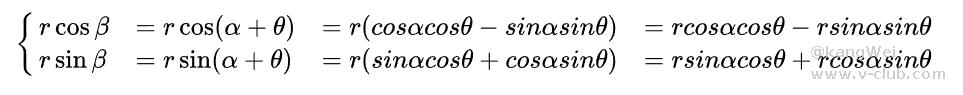
写成矩阵形式为 

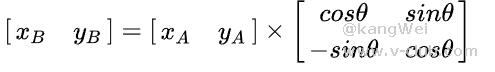
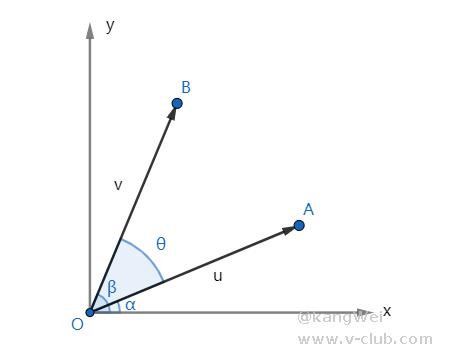
上式θ可由鼠标前后位置与圆心所成向量的夹角变化表示，即如下图dθ所示  

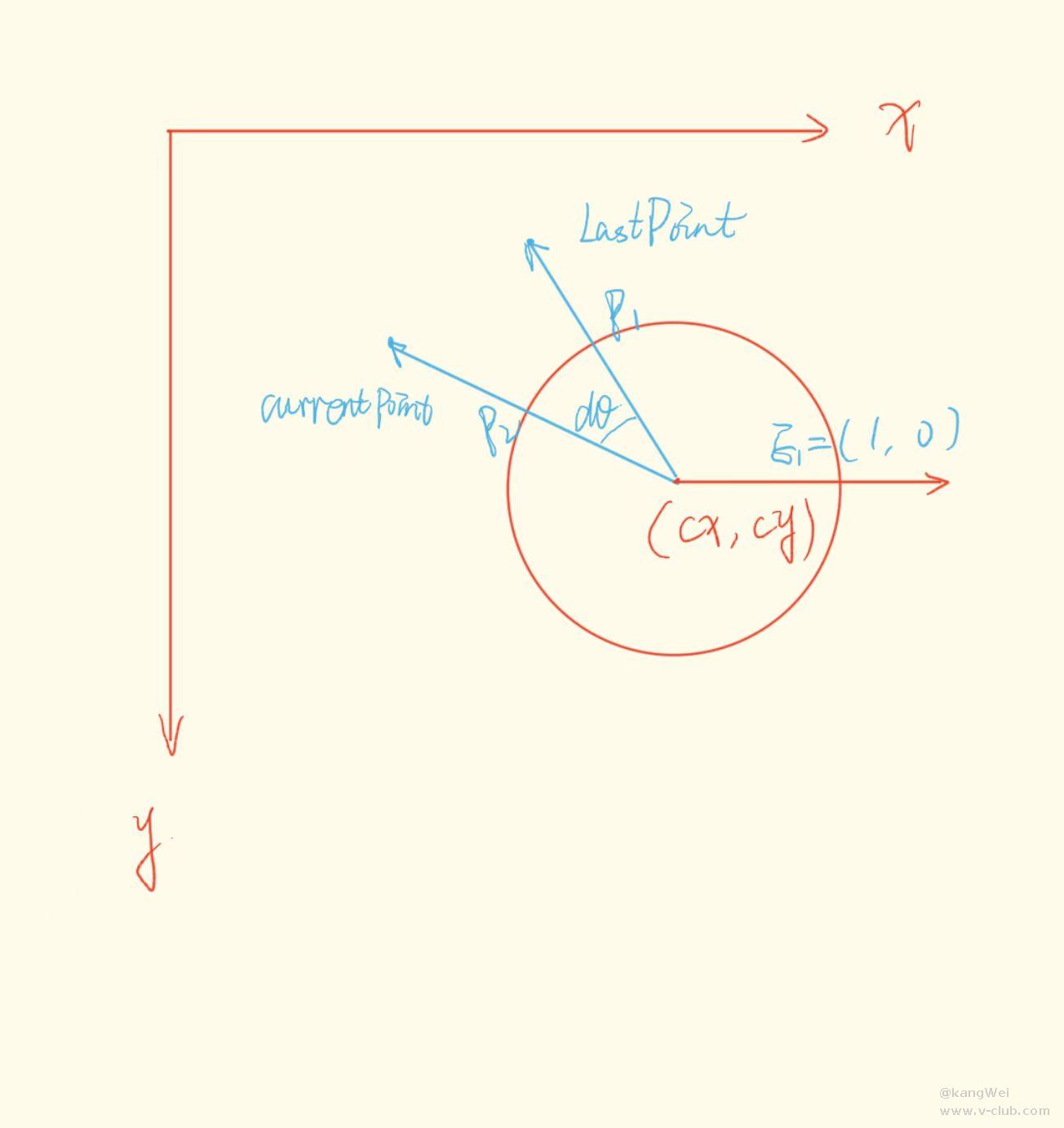
在理想状态，不考虑精度损失的情况下，求出OB向量后，将OB向量加上O点坐标，即可得扇形边界点旋转后的坐标。  
但由于CPoint是int型，而旋转过程中计算所用sin、cos函数均为float或double型，存在较大精度损失，故实际转换后的扇形边界点需计算OB向量与圆O的交点，再根据交点的远近，选择离A点最近的交点作为扇形边界点的新值。

2.代码实现

void getCrossLineCircle(double k, double b, CPoint centerPoint, float r, CPoint* returnPoint) {
	double a = pow(k, 2) + 1;
	double b1 = 2 * (k * b - k * centerPoint.y - centerPoint.x);
	double c = pow(centerPoint.x, 2) - (double)r * r + pow(b - centerPoint.y, 2);

	double x1 = (-b1 + sqrt(pow(b1, 2) - 4 * a * c)) / 2 / a;
	double y1 = k * x1 + b;
	double x2 = (-b1 - sqrt(pow(b1, 2) - 4 * a * c)) / 2 / a;
	double y2 = k * x2 + b;

	returnPoint[0] = CPoint(x1, y1);
	returnPoint[1] = CPoint(x2, y2);

}

void transPoint1(double dxita, CPoint* startPoint, CPoint centerPoint, float r) {
	CPoint rotatedVec(startPoint->x - centerPoint.x, startPoint->y - centerPoint.y);

	double endRotatedVecX = rotatedVec.x * cos(dxita) - rotatedVec.y * sin(dxita);
	double endRotatedVecY = rotatedVec.x * sin(dxita) + rotatedVec.y * cos(dxita);

	CPoint temp[2];
	if (endRotatedVecX == 0) {
		temp[0] = CPoint(centerPoint.x, centerPoint.y + r);
		temp[1] = CPoint(centerPoint.x, centerPoint.y - r);
	}
	else if (endRotatedVecY == 0) {
		temp[0] = CPoint(centerPoint.x + r, centerPoint.y);
		temp[1] = CPoint(centerPoint.x - r, centerPoint.y);
	}
	else {
		double k = endRotatedVecY / endRotatedVecX;
		double b = (double)centerPoint.y - k * centerPoint.x;

		getCrossLineCircle(k, b, centerPoint, r, temp);
	}

	if (temp[0].x - startPoint->x >= -r && temp[0].x - startPoint->x <= r && temp[0].y - startPoint->y >= -r && temp[0].y - startPoint->y <= r) {
		startPoint->x = temp[0].x;
		startPoint->y = temp[0].y;
	}
	else {
		startPoint->x = temp[1].x;
		startPoint->y = temp[1].y;
	}
	return;
}

//计算旋转角度
CPoint startVec(m_lastButtonDownPoint->x - m_pieLink->m_currentHoverNode->data->center.x, 
		m_lastButtonDownPoint->y - m_pieLink->m_currentHoverNode->data->center.y);
CPoint endVec(	currentPoint->x - m_pieLink->m_currentHoverNode->data->center.x,
		currentPoint->y - m_pieLink->m_currentHoverNode->data->center.y);
float startxita = getAngleToXPositive(startVec);
float endxita = getAngleToXPositive(endVec);

if (startxita != endxita) {	//未做旋转，则不需要修改startPoint
	float dxita = endxita - startxita;

	int r1 = m_pieLink->m_currentHoverNode->data->maxRectBoundary.right - m_pieLink->m_currentHoverNode->data->center.x;
	transPoint1(dxita, m_pieLink->m_currentHoverNode->data->anglePoint, m_pieLink->m_currentHoverNode->data->center, r1);
	int r2 = m_pieLink->m_currentHoverNode->data->minRectBoundary.right - m_pieLink->m_currentHoverNode->data->center.x;
	transPoint1(dxita, m_pieLink->m_currentHoverNode->data->anglePoint + 1, m_pieLink->m_currentHoverNode->data->center, r2);
}

3.效果如下

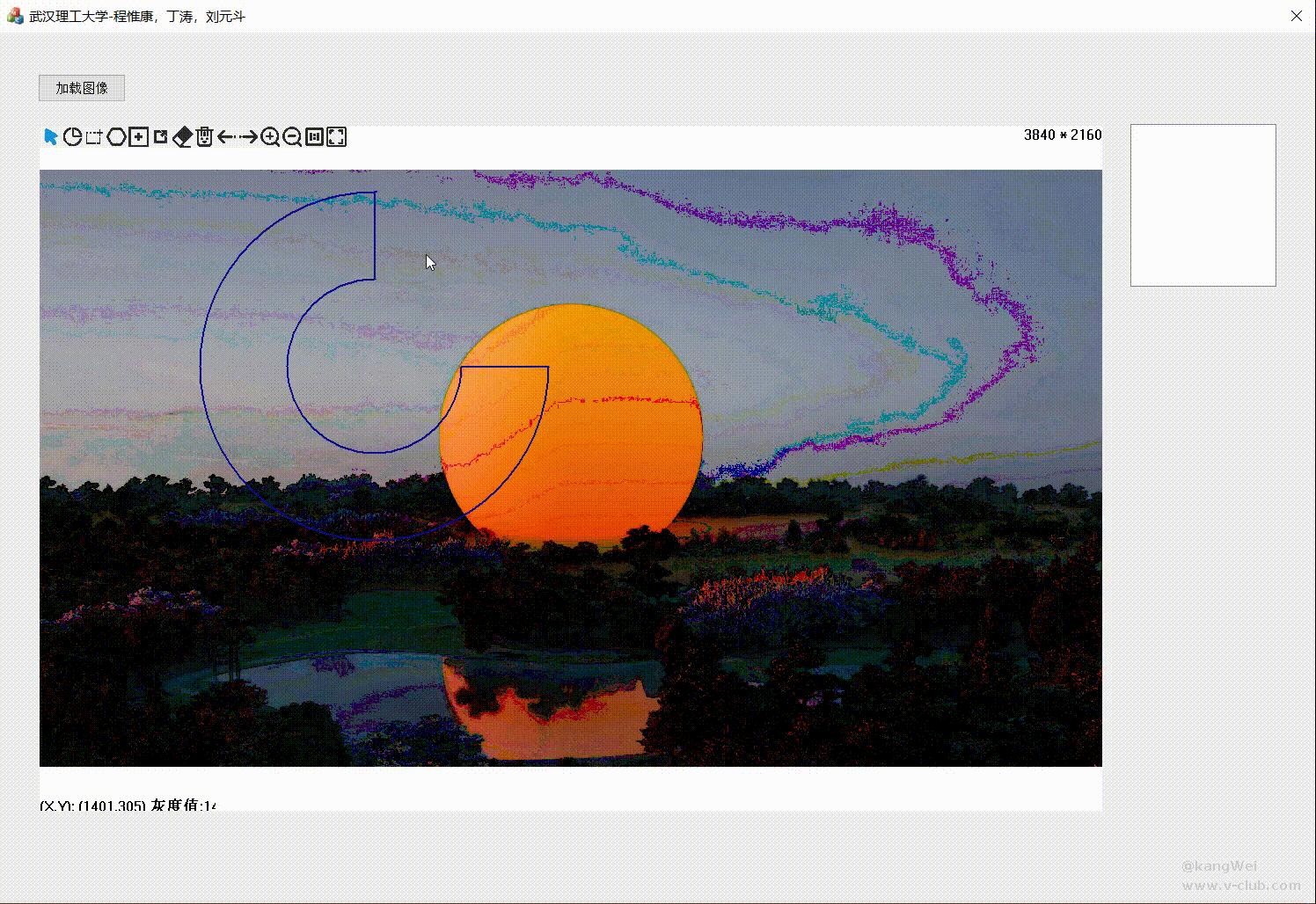
此方法仍旧存在一点小瑕疵，内外圆旋转存在角度偏差，旋转越久，偏差越明显。

四.结语

写博客的次数不多，可能存在许多表述不明、表述有误的地方，欢迎大家批评指正。