圆拟合算法剖析与硬核实战

• 什么是圆拟合
• 定义
• 特征
• 主流算法
• 最小二乘法（LS）
• 原理
• 核心代码
• 迭代重加权最小二乘法（IRLS）
• 原理
• 核心代码
• 非线性优化法(GN)
• 原理
• 核心代码
• 运行结果对比

什么是圆拟合

顾名思义，圆拟合是从给定的点集数据中拟合出一个圆。

定义

通过一堆离散的点，然后根据这些离散点的特点，拟合出一个圆。

特征

1. 一堆离散的点，点数大于等于2；
2. 离散点的特征，满足几何基元约束；
3. 拟合出一个圆，结果一定是个圆。

主流算法

机器视觉（或是计算机视觉）领域，主流的圆拟合算法有：

1. 最小二乘法
2. 迭代重加权最小二乘法
3. 非线性优化法
4. 旋转角度法
5. 旋转角度最小二乘法

后面两种算法仅用于小角度圆拟合场景，严格意义上讲不属于典型圆拟合范畴，因此本文不做介绍。

最小二乘法（LS）

原理

圆的标准方程为：

$(r-a)^2+(c-b)^2=R^2$

展开可得：

$2ra+2cb-a^2-b^2+R^2=r^2+c^2$

令$q=a^2+b^2-R^2$，则有：


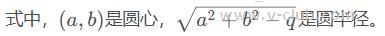
误差函数：

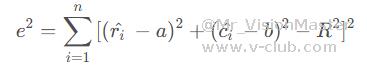
定义矩阵A：

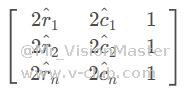
定义矩阵B：

则根据最小二乘法有：

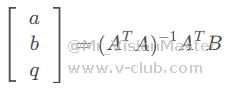
核心代码

double A_matrix[MAX_POINT_NUM] = { 0.0 };
double B_matrix[MAX_POINT_NUM] = { 0.0 };
double x_matrix[3] = { 0.0 };

for (int i = 0; i < nPointArrayCount; i++)
{
	A_matrix[i * 3 + 0] = 2 * fFitPointX[i];
	A_matrix[i * 3 + 1] = 2 * fFitPointY[i];
	A_matrix[i * 3 + 2] = 1;
	B_matrix[i] = pow(fFitPointX[i], 2) + pow(fFitPointY[i], 2);
}
int nRet = LeastSquare(A_matrix, B_matrix, x_matrix, nPointArrayCount);

fCenterX = x_matrix[0];
fCenterY = x_matrix[1];
fRadius = sqrt(pow(x_matrix[0], 2) + pow(x_matrix[1], 2) + x_matrix[2]);

迭代重加权最小二乘法（IRLS）

原理

最小平方圆拟合对于离群值不够鲁棒，因此需要引入权重并使用它来减小离群值的影响。先采用正常的最小二乘法拟合一个圆，然后用各拟合点到此圆的距离来计算在后续的迭代中将使用的各点所对应的权重。
误差函数：

式中，$(a,b)$是圆心，$R$是圆半径，$w_{i}$是权重函数。
第一种权重函数为Huber权重函数：

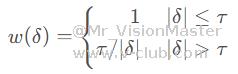
式中，$\delta$为拟合点到圆周的距离，$\tau$为削波因数。所有距离$\leq\tau$的点对应的权重都是1，距离$>\tau$的点将分配更小的权重，从而减小离群点对结果的干扰。
第二种权重函数为Tukey权重函数：

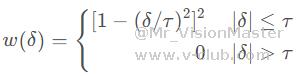
式中，$\delta$为拟合点到圆周的距离，$\tau$为削波因数。所有距离$\leq\tau$的点对应的权重在1~0之间平滑变化，距离$>\tau$的点将被完全忽略，不参与拟合，从而减小离群点对结果的干扰。
削波因数$\tau$的计算公式为：

$\sigma_{\delta}=\frac{median|\delta_{i}|}{0.6745}$

$\tau=2\sigma_{\delta}$

对于符合正态分布的离群值，鲁棒标准偏差$\sigma_{\delta}$的分子为所有拟合点到圆心距离的中值，分母为基于正态分布计算的标准偏差。

核心代码

此处代码不做展示，留作读者自行实现。

非线性优化法(GN)

原理

将所有拟合点到待拟合圆的平方距离进行连加求和，然后使求得的总和最小化。
误差函数：

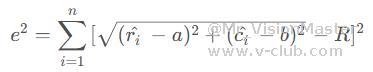
式中，$(a,b)$是圆心，$R$是圆半径。与之前的方法不同，这是一个非线性优化的问题，只能采用非线性优化技术来求解。
常见的非线性优化算法有：

1. 梯度下降法
2. 牛顿法
3. 拟牛顿法
4. 高斯牛顿法
5. 列文伯格-马夸尔特法

其中，高斯牛顿法（Gauss–Newton algorithm）在牛顿法的基础上做了改进。牛顿法中的H矩阵需要计算目标函数的二阶偏导，计算量巨大，高斯牛顿法采用G矩阵替代H矩阵，大大减小了计算量。
因此，选择高斯牛顿法实现圆拟合的非线性优化。

核心代码

// 开始Gauss-Newton迭代
int iterations = 20;            // 迭代次数
double cost = 0, lastCost = 0;  // 本次迭代的cost和上一次迭代的cost

// CostFunction = Σ(AXi - Bi)²  A=(a,b,c) Xi=(xi,yi,1)^T Bi = -xi² - yi²
for (int iter = 0; iter < iterations; iter++) {
	Matrix3d H = Matrix3d::Zero();             // Hessian = J^T W^{-1} J in Gauss-Newton
	Vector3d b = Vector3d::Zero();             // bias
	cost = 0;

	for (int i = 0; i < N; i++) {
		double xi = x_data[i], yi = y_data[i];  // 第i个数据点
		double error = xi * xi + yi * yi + (ae * xi + be * yi + ce);
		Vector3d J; // 雅可比矩阵
		J[0] = xi;  // de/da
		J[1] = yi;  // de/db
		J[2] = 1;   // de/dc

		H += J * J.transpose();
		b += -error * J;

		cost += error * error;
	}

	// 求解线性方程 Hx=b
	Vector3d dx = H.ldlt().solve(b);
	if (isnan(dx[0])) {
		cout << "result is nan!" << endl;
		break;
	}

	if (iter > 0 && cost >= lastCost) {
		cout << "cost: " << cost << ">= last cost: " << lastCost << ", break." << endl;
		break;
	}
	
	ae += dx[0];
	be += dx[1];
	ce += dx[2];

	lastCost = cost;

	cout << "total cost: " << cost << ", \t\tupdate: " << dx.transpose() <<
		"\t\testimated params: " << ae << "," << be << "," << ce << endl;
}

double centerX = ae / -2;
double centerY = be / -2;
double radius = sqrt(ae * ae / 4 + be * be / 4 - ce);

运行结果对比

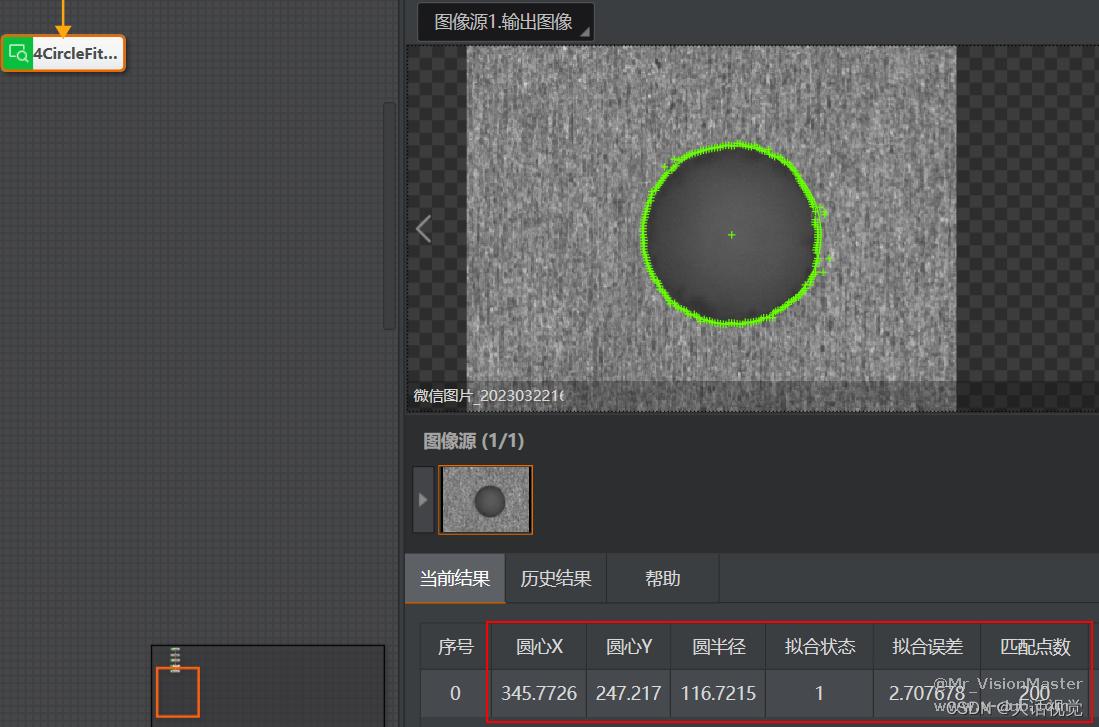
采集多组独立的数据，分别采用本文提出的算法、VisionMaster（国内最领先的算法平台，简称VM）进行圆拟合，从圆拟合结果（含拟合误差）、算法运行耗时两个方面评估算法的准确性和效率性。
VM圆拟合结果：

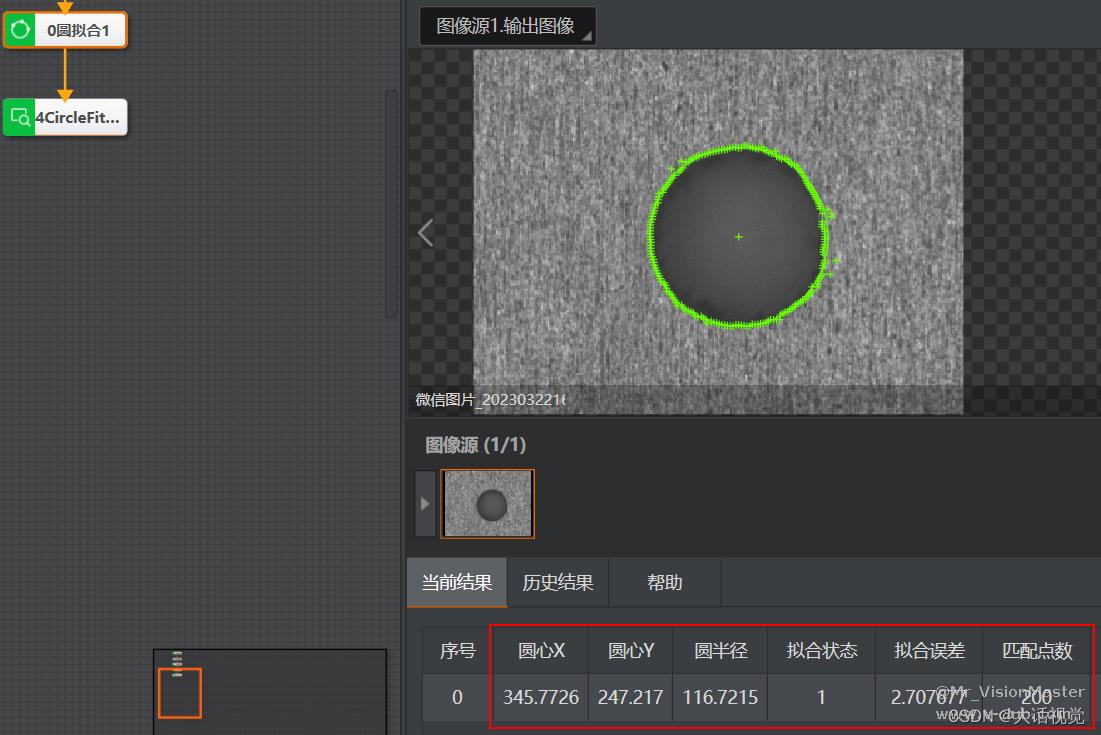
本文圆拟合结果：

算法运行耗时：

可以看出，算法准确性方面，本文提出的算法足以媲美VM；算法效率性方面，在拟合点数为200个点时，本文提出的算法运行耗时稳定在0.23ms内，亦可媲美VM。
当然，能够在一个小小的算法性能上追赶VM，就是小编最值得骄傲的事情啦！小编衷心希望国产品牌能够扬名世界，而我们每个人亦能为国产产品做出自己的贡献与创新，不断突破国外垄断和技术壁垒。