模型在训练集样本上的训练误差，可以根据每批次样本的误差函数做精确计算，也可以根据正负样本的预测情况获得准确的召回率；而在使用模型预测时，我们需要能凭借一些角度标准，来评估模型在海量测试集内的实际误差，也称之为泛化误差。

    在谈到损失，误差，性能等问题时，其实也是在讨论模型的拟合程度，需要避免欠拟合和过拟合的情况。举个例子，同学A往往有自己的学习方法，通过往年习题提升自身能力，同学B会生硬的记住往年习题的答案，同学C就只看了部分习题答案且学习时间很短。那么同学B在做往年习题时的答题内容是相当”完美”的，但一旦遇到考试真题，会生搬硬套的将习题答案抄到相似考题上（过拟合）。同学A由于具备泛化能力，可以通过考题透露的信息推演答题方向，即便他在作答往年习题时表现的并不”完美”。同学C则无论面对哪种题目，都会表现的最差（欠拟合）。

    但是，泛化误差是一个需要在海量数据集上才能计算出的数值，依据样本获取难度和人力测试成本，我们无法对其进行准确预估。那么我们应该去了解影响泛化误差的因素：1. 网络规模。2. 附加惩罚项。3.训练样本量。
    其中，第1项网络规模受超参和常参数量限制，如学习率，迭代次数，模型大小，patch大小，剪枝系数等，是影响模型整体精度的因素之一，下图为相同迭代不同网络规模下，训练误差与泛化误差的理想关系，为避免此情况，大型网络中往往会对输出函数施加惩罚项，这也是第2项需要做的工作，以达到权重衰减的目的，此处暂不详细讨论；

    第3项样本量的大小是最为重要的因素，当训练集中的样本越少，越可能遇到过拟合情况。随着标注科学的训练数据量增加，泛化误差会减小，这很容易理解，正确丰富的数据信息使模型应用更具鲁棒性，下图为相同迭代不同样本量下，训练误差与泛化误差的理想关系。

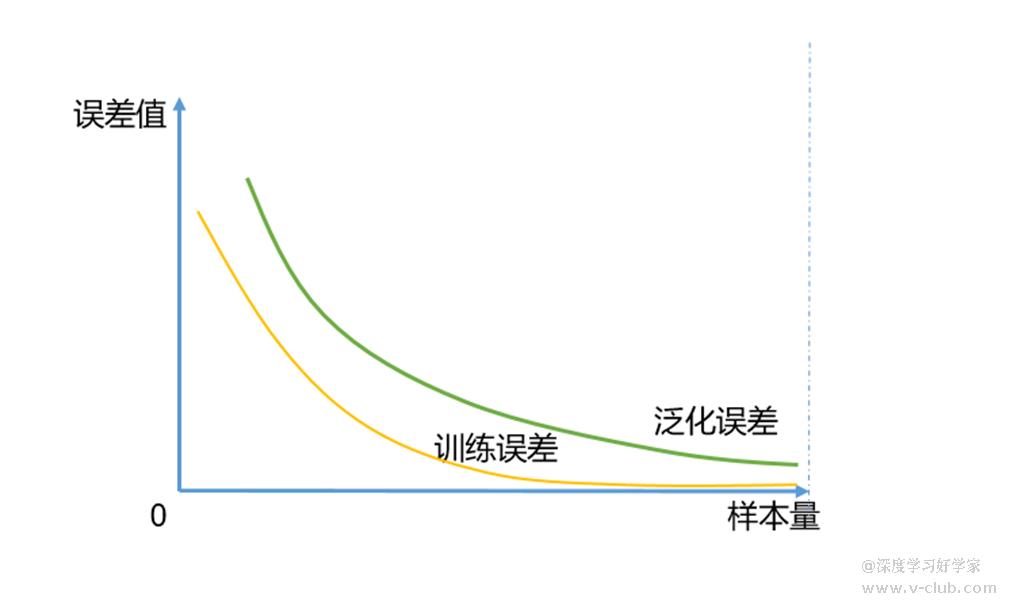
    在实际应用中，可能也会发现样本量增加后效果反而变差的情况，这就需要回到训练集上重新审查：1.是否缺陷或目标形态过于单一的情况，比如同一个检出对象在不同位置的样本类型，或者重复使用的缺陷样本；2.是否标注不合理，比如有漏标、误标的情况；3.是否存在类别占比严重失衡，比如在训练集中只对一张图定义了类别X，其它类别在训练集中的占比远超于X的情况。

        
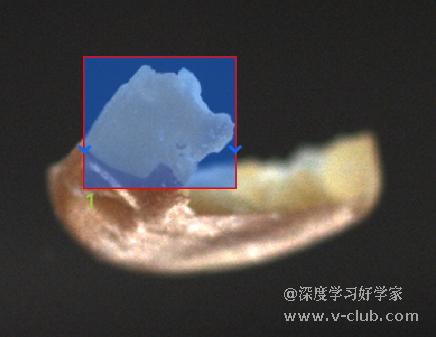
                                                     1类情况：样本旋转，目标形态单一       

    
                                                                    2类情况：误标或漏标                                                                        

    
                                                                       3类情况：类别失衡

    当我们了解到样本量的重要性后，就可以理解，少量训练样本下的泛化误差通常比较高，一般无法直接应用于海量测试集中，目标形态与分类程度越复杂，需要的样本量越多。在工业场景中，经常需要在小样本下实现较好的测试集检出率，这就需要优化网络结构，或者算法沿用海量数据泛化的基础模型参数，或者通过人为方法制造缺陷。但无论如何，有监督学习目前仍是要不断增加样本并迭代模型，这是一个过程。可以考虑用传统算法或无监督学习在前期做为NG筛选器，以积累NG样本，后续转为有监督预测。