运动学定义

运动学，从字面上理解就是研究运动特征的一门学科，具体来讲，运动学通过几何学研究物体在某一坐标系下位姿随时间变化的规律，且不考虑力和物体自身物理性质。本文后续的内容将围绕移动机器人对运动学基础知识展开讲解。

运动学模型

在上一节的定义中提到，运动学的研究不考虑力和物体自身的物理性质，所以运动学的模型也对物体的部分性质做了理想化和抽象化的处理，基本分类可参考下图：

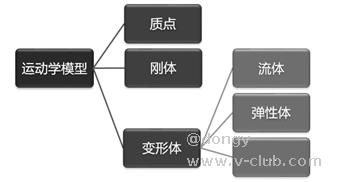
质点：没有形状和质量、但在空间占据一定位置的几何点，内部不存在相对运动。可研究运动方程、轨迹、位移、速度、加速度等运动特征。

刚体：没有质量，但是具有一定形状，占据一定空间且不产生形变的形体。内部可视为由大量质点组成，质点间不存在相对运动。挑选内部一点代表整个刚体， 除质点本身具备的运动特征外，还可以研究刚体的转动过程、角速度、角加速度等更复杂的运动特征。

变形体：会在外力下产生形变的形体的统称。在实际应用中，一般在工程上确保移动机器人的形变可被忽略，所以本文不展开讨论变形体的特征。

1.3      运动特性

根据上一小节的介绍，不难发现移动机器人通常可视为刚体，因为其本身的形状和转动不可被忽略。刚体的运动特性又可分为如下几类：

（1）平动：刚体内两点所连成的直线在移动过程中保持平行，即不存在任何姿态变化，可视为质点；

（2）定轴转动：刚体绕内部一条固定直线转动；

（3）定点转动：刚体绕固定一点转动；

（4）平面运动：刚体内部任意一点与某一固定平面距离保持不变的运动；

（5）一般运动：刚体在空间内自由运动，不存在任何约束。

1.4      基本原理

用刚体描述移动机器人意味着在研究过程中可以利用刚体的性质，在对运动特征进行研究前需要了解一些相关的基本原理和方法。

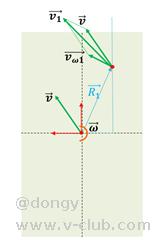
（1）速度投影定理

刚体上任意两点的速度不一定相同，但两点的速度在沿着其连线方向上的投影必定相同。如下图，假设现在两点分别具有线速度，两者在连线上的分量必定相等：

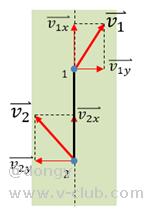
（2）速度瞬心法

刚体在做平面运动且具有一定角速度时，都可以从该平面中找到一点作为瞬心(ICR)；瞬心的速度为0，这一时刻刚体上的所有点都可视为绕瞬心进行旋转运动，各点角速度相同。当刚体角速度为0时瞬心视为在无穷远处。

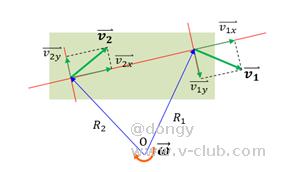
（3）阿克曼转向原理

为了保证移动机器人在运动过程中每组舵轮都处于纯滚动状态，在转向时各组舵轮轴线都必须交于同一点(瞬心)，下图为一般汽车阿克曼结构底盘(前轮转向，后轮定向)受到的约束。

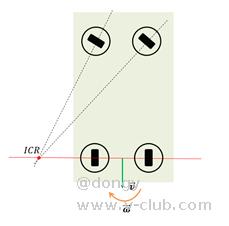
（4）基点法

刚体做平面运动时，任一时刻刚体的运动可分解为刚体上任意一点（基点）的“旋转运动“+”平移运动”。如下图所示：